Isn’t it amazing, if you can calculate faster in competitive exams or in daily life? In competitive exams you need to solve more number of problems in less time. So, people, nowadays running behind the coaching centers for shortcuts. But it is absolutely useless if you don’t have conceptual clarity. Here is the speed math rule for adding large numbers. Check other quicker math rules here.
Adding large numbers just in your head can be difficult. This method shows how to simplify this process by making all the numbers a multiple of 10. Here is an example:
644 + 238 = ?
While these numbers are hard to contend with, rounding them up will make them more manageable. So, 644 becomes 650 and 238 becomes 240.
Now, add 650 and 240 together. The total is 890. To find the answer to the original equation, it must be determined how much we added to the numbers to round them up.
650 – 644 = 6 and 240 – 238 = 2
Now, add 6 and 2 together for a total of 8
To find the answer to the original equation, 8 must be subtracted from the 890.
890 – 8 = 882
So the answer to 644 +238 is 882.
This is speed math trick 8. Please check other speed math tricks here.
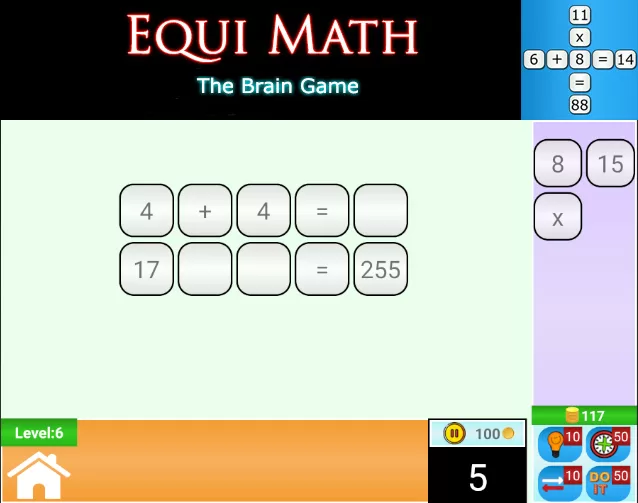
Are you ready to play a brain game? Ok, that’s Equi Math for you. Click here to get the Android Game. This game will help in decision making in quick time. It is very easy at beginning and gets difficult on the higher levels. Try to reach as much higher level as possible. On game over, try again to improve your best. That way you will have quick solving skills.
Write down your feedback on comments section below.
Don’t forget to share. Please subscribe to Mathkind here for math tricks and help.